অধ্যায় ১ ঃ সংখ্যা
বাস্তব সংখ্যা || বিগত নিয়োগ পরীক্ষার MCQ সহ বিস্তারিত আলোচনা
বাস্তব সংখ্যা দ্বারা শুধুমাত্র সংখ্যাকে নির্দেশ করলে ও এটি আমাদের জীবনের অত্যন্ত গুরুত্বপূর্ণ একটি দিক। সংখ্যা আমাদের জীবনের বিভিন্ন ক্ষেত্রে সহায়তা করে, সংখ্যা ব্যবহার করে আমরা ব্যাক্তিগত জীবন থেকে শুরু করে প্রকৃতি ও বিজ্ঞানের জগত পর্যন্ত পর্যালোচনা করে থাকি। উদাহরণস্বরূপ, একটি মানুষের উচ্চতা, ওজন, বয়স ইত্যাদি সংখ্যার মাধ্যমে প্রকাশ করা হয়। আর আর্থিক দিক থেকে বললে, আমাদের প্রতিটি আর্থিক লেনদেন বা লেনদেনের বিবরণ একটি সংখ্যার মাধ্যমে প্রকাশ করা হয়।যাই হোক বিভিন্ন প্রতিযোগিতামূলক পরীক্ষার জন্য বাস্তব সংখ্যা খুবই গুরুত্বপূর্ণ।বাস্তব সংখ্যার পরিপূর্ণ ধারণা ছাড়া গণিতের সমস্যার সমাধান করতে পারব না। আজকের পাঠে আমরা এটি নিয়ে এ টু জেড পরিষ্কার ধারণা দেয়ার চেষ্টা করব। সর্বশেষে আমরা এই অধ্যায়ে বিগত সালের প্রশ্ন অনুশীলন করার সুযোগ করে দিয়েছি। যা আপনার প্রস্তুতিতে সহায়ক ভূমিকা পালন করবে বলে আমাদের বিশ্বাস।
অংক ও সংখ্যা
অংকঃ Digit অর্থ অংক।মানুষ হিসাব নিকাশ ও গণনা কার্যের জন্য যে সকল প্রতীক বা চিহ্ন ব্যবহার করে সেগুলোই অংক। গণিতে ০ থেকে ৯ পর্যন্ত মোট ১০টি অংক রয়েছে। অংক দুই ধরনের যথা-
১। সার্থক অংক—১,২,৩,৪,৫,৬,৭,৮,৯ ।
২। সহকারী অংক— ০ ।
সংখ্যা (Number): অংক দ্বারা পরিমাণ বুঝালে সংখ্যা হবে।এক বা একাধিক অংক মিলে সংখ্যা তৈরি হয়।একক অংক হিসেবে পরিমাণজ্ঞাপক হলে সার্থক অংকগুলোকে সংখ্যা বলা হয়।অর্থাৎ ১,২,৩,৪,৫,৬,৭,৮,৯ অংকগুলো দ্বারা পরিমাণ বোঝালে সেগুলোকে সংখ্যাও বলা হয়।
স্বাভাবিক সংখ্যা (Natural Number): ১,২,৩,৪,… ইত্যাদি স্বাভাবিক সংখ্যা। অর্থাৎ ১ থেকে শুরু অসীম।যার কোন শেষ নেই।তবে এগুলোকে ধনাত্নক বা ঋণাত্নক বলে চিহ্নিত করা হয় না। এগুলো সবসময় স্বাভাবিক । স্বাভাবিক সংখ্যার সেটকে N দ্বারা প্রকাশ হয়।
মৌলিক সংখ্যা ( Prime Number ): যে সংখ্যাকে শুধু ১ এবং ঐ সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না তাকে মৌলিক সংখ্যা বলে। আরো সহজভাবে বললে, যে সংখ্যাকে অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না তাকে মৌলিক সংখ্যা বলে। যেমনঃ ৩১ একটি মৌলিক সংখ্যা। উল্লেখ্য, ১ মেীলিক সংখ্যা নয়, যেহেতু এর উৎপাদক ১টি।মেীলিক সংখ্যার দুইটি উৎপাদক থাকে যথা ১ এবং ঐ সংখ্যা নিজে।ঋণাত্নক সংখ্যা কখনো মৌলিক হতে পারে না এবং মৌলিক সংখ্যা ২ থেকে শুরু হয়। একমাত্র জোড় মৌলিক সংখ্যা হল ২ ।
১ থেকে ১০০ পর্যন্ত মোট ২৫টি মৌলিক সংখ্যা এবং ১০১ থেকে ২০০ পর্যন্ত মোট ২১টি মৌলিক সংখ্যা রয়েছে।
১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা
১০১ থেকে ২০০ পর্যন্ত মৌলিক সংখ্যা
মৌলিক ও অন্যান্য সংখ্যা
মৌলিক দ্বিজোড়: পরস্পর দুটি মৌলিক সংখ্যার ব্যবধান ২ হলে তাকে মৌলিক দ্বিজোড় বলে।যেমন-৫,৭,১১,১৩ ইত্যাদি। ১ থেকে ১০০ পর্যন্ত ৮টি মৌলিক দ্বিজোড় রয়েছে।
মৌলিক ত্রিজোড়: পরস্পর তিনটি মৌলিক সংখ্যার অন্তর ২ হলে তাদের মৌলিক ত্রিজোড় বলে।যেমন- ৩,৫,৭ ।
যৌগিক সংখ্যাঃ যে সকল সংখ্যাকে ১ এবং সেই সংখ্যা ছাড়াও অন্য এক বা একাধিক সংখ্যা দ্বারা ভাগ করা যায় তাকে যৌগিক সংখ্যা বলে।যেমন- ৪,৬,৮,৯,১০ ইত্যাদি।
সহমৌলিক সংখ্যা ( Co-Prime number ) : দুইটি স্বাভাবিক সংখ্যার গ.সা.গু. ১ হলে তাদেরকে পরস্পরের সহমৌলিক বলা হয়। যেমন ৮ ও ১৫ পরস্পর সহমৌলিক । কারণ এদের গ.সা.গু. ১ ।তবে সংখ্যা মৌলিক বা যৌগিক যাই হোক না কেন সংখ্যাগুলোর গ.সা.গু বাদ দিয়ে যে উৎপাদকগুলো থাকে তা সর্বদা সহমৌলিক।উদাহরণস্বরুপ- ২০ ও ১৫। ২০ এর উৎপাদক হল ১,২,৪,৫,২০ এবং ১৫ এর উৎপাদক হল ১,৩,৫,১৫।এখানে ১ বাদে উভয়সংখ্যার উৎপাদকগুলো পরস্পরের সহমৌলিক।
জোড় ও বিজোড় সংখ্যা (Even & Odd number): যে সমস্ত সংখ্যা ২ দ্বারা ভাগ করা যায় অর্থাৎ যে সমস্ত সংখ্যার এককের ঘরের অঙ্ক ২, ৪, ৬, ৮ বা ০ তারা জোড় সংখ্যা। যেমন—২, ৫৪, ১৫৬, ৯০৯৮, ১৫৮৩৪০, ইত্যাদি। উল্লেখ্য, ০ একটি জোড় সংখ্যা। আবার যে সব সংখ্যা ২ দ্বারা ভাগ করা যায় না অর্থাৎ যে সব সংখ্যার এককের ঘরের অঙ্ক ১, ৩, ৫, ৭ বা ৯, তারা বিজোড় সংখ্যা। শুধু কোন অক্ষর যেমন- X, Y, Z জোড় সংখ্যা না আবার বিজোড় সংখ্যা ও না।আপনি যখন যাকে যা ধরবেন,তা-ই হবে। কিন্তু জোড় কিংবা বিজোড় যেকোনো সংখ্যাকেই ২ বা যেকোন জোড়সংখ্যা দ্বারা গুণ করলে গুণফল সবসময়ই জোড় সংখ্যা হয়।যেমন-2X জোড় নাকি বিজোড়? এখানে X এর মান বিজোড় সংখ্যা ১ ধরলে 2X এর মান ২ যা জোড় সংখ্যা।আবার X এর মান জোড় সংখ্যা ২ ধরলে 2X এর মান হয় ৪। এটিও জোড় সংখ্যা।কিন্তৃ বিজোড় সংখ্যা দিয়ে জোড় সংখ্যাকে গুণ করলে গুণফল জোড় হয়।আবার বিজোড় সংখ্যা দিয়ে বিজোড় সংখ্যাকে গুণ করলে গুণফল বিজোড় হয়।
পূর্ণসংখ্যা (Integer): যে সমস্ত সংখ্যার কোন ভগ্নাংশ থাকে না তাদেরকেই পূর্ণ সংখ্যা বলে । আরো সহজভাবে বললে, শূন্যসহ সকল ধনাত্মক ও ঋণাত্মক অখন্ডক সংখ্যাকে পূর্ণসংখ্যা বলে। যেমন: ......৩,-২,-১,০,১,২,৩.......ইত্যাদি। পূর্ণসংখ্যার সেটকে Z দ্বারা প্রকাশ হয়। পূর্ণসংখ্যার সংখ্যা অসীম।
ভগ্নাংশ সংখ্যা (Fractional Number)
ভগ্নাংশ : কোন বস্তু বা পরিমাণের অংশ বা ভাগ নির্দেশ করতে যে সংখ্যা শ্রেণি ব্যবহৃত হয় তাকে ভগ্নাংশ সংখ্যা বলে। যেমন- ।
ভগ্নাংশ প্রধানত দুই প্রকার যথা- ১। সাধারণ ভগ্নাংশ ২। দশমিক ভগ্নাংশ।
সাধারণ ভগ্নাংশ: যে সব সংখ্যাকে আকারে প্রকাশ করা যায় তাকে সাধারণ ভগ্নাংশ সংখ্যা বলে।সাধারণ ভগ্নাংশের উদাহরণ- ।
সাধারণ ভগ্নাংশ আবার তিন প্রকার যথা- ১। প্রকৃত ভগ্নাংশ ২। অপ্রকৃত ভগ্নাংশ ৩। মিশ্র ভগ্নাংশ।
প্রকৃত ভগ্নাংশ: যে সব ভগ্নাংশের হর বড় এবং লব ছোট তাকে প্রকৃত ভগ্নাংশ বলে।উল্লেখ্য, ভগ্নাংশের নিচের সংখ্যাটিকে হর এবং উপরের সংখ্যাটিকে লব বলে।যেমন- ।
অপ্রকৃত ভগ্নাংশ: যে সব ভগ্নাংশের হর ছোট এবং লব বড় তাকে অপ্রকৃত ভগ্নাংশ বলে।যেমন- ।
মিশ্র ভগ্নাংশ: পূর্ণসংখ্যার সাথে প্রকৃত ভগ্নাংশ যুক্ত থাকলে তাকে মিশ্র ভগ্নাংশ বলে। যেমন- ।
দশমিক ভগ্নাংশ
দশমিক ভগ্নাংশ: যে ভগ্নাংশকে দশমিক (.) চিহ্নের সাহায্যে প্রকাশ করা হয়, তাকে দশমিক ভগ্নাংশ বলে। দশমিক বিন্দুর আগের অংশ পূর্ণসংখ্যা এবং পরের অংশ ভগ্নাংশ । দশমিক বিন্দু থেকে বামদিকের অঙ্কগুলোর স্থানীয় মন পর্যায়ক্রমে একক, দশক , শতক ইত্যাদি। এবং ডানদিকের অঙ্কগুলোর স্থানীয় মান পর্যায়ক্রমে দশমাংশ, শতাংশ, সহস্রাংশ ইত্যাদি।দশমিক ভগ্নাংশ দুই প্রকার যথা- সসীম দশমিক ও অসীম দশমিক।অসীম দশমিক আবার দুই প্রকার যথা অসীম আবৃত এবং অসীম অনাবৃত।
সসীম দশমিক ভগ্নাংশ: যে সংখ্যাকে ভাগ করলে দশমিক বিন্দুর পরের সংখ্যাগুলো সসীম বা নির্দিষ্ট ফলাফল বের হয়ে শেষ হয়ে যায়, এমন ভগ্নাংশকে সসীম দশমিক ভগ্নাংশ বলে। যেমনঃ ৩.৫। এখানে, দশমিক সংখ্যার পর একটা নির্দিষ্ট সংখায় বের হয়ে ভাগ শেষ হয়ে গেছে মানে দশমিক সংখ্যাটা সসীমতায় আছে। তাই একে সসীম দশমিক ভগ্নাংশ বলে।
অসীম আবৃত দশমিক ভগ্নাংশ: যেসব দশমিক ভগ্নাংশে দশমিক বিন্দুর ডানে একটি অঙ্ক ক্রমান্বয়ে বারবার বা একাধিক অঙ্ক পর্যায়ক্রমে বারবার আসে, তাদের আবৃত বা পৌনঃপুনিক দশমিক ভগ্নাংশ বলে। আবৃত বা পৌনঃপুনিক দশমিক ভগ্নাংশে যে অংশ বারবার অর্থাৎ পুনঃপুনঃ হয়, তাকে আবৃত অংশ বলে। যেমন: ৩.৩৩৩৩..., ১০.২৩৪৫৬৪৫৬... ইত্যাদি আবৃত বা পৌনঃপুনিক দশমিক ভগ্নাংশ।
অসীম অনাবৃত দশমিক ভগ্নাংশ: যে অসীম দশমিক ভগ্নাংশে দশমিক চিহ্নের ডানদিকের অঙ্ক কখনো শেষ হয় না, অর্থাৎ দশমিক চিহ্নের ডানদিকের অঙ্কগুলো সসীম হবে না অথবা অংশবিশেষ বারবার আসবে না। যেমন : 1.4142135......,
2.8284271..... ইত্যাদি অসীম অনাবৃত দশমিক ভগ্নাংশ। সসীম দশমিক ও আবৃত্ত দশমিক ভগ্নাংশ মূলদ সংখ্যা এবং অসীম অনাবৃত দশমিক ভগ্নাংশ অমূলদ সংখ্যা। সহজ কথায় অসীম অনাবৃত দশমিক বাদে বাকি সবই মূলদ সংখ্যা। একমাত্র এটিই অমূলদ সংখ্যা।
মূলদ ও অমূলদ সংখ্যা
মূলদ সংখ্যা (Rational Number): আকারের যেকোনো সংখ্যাকে মূলদ সংখ্যা বলে, যখন p ও q পূর্ণসংখ্যা এবং q ≠ 0। যেকোনো মূলদ সংখ্যাকে দুইটি সহমৌলিক সংখ্যার অনুপাত হিসেবে ও লেখা যায়। সকল পূর্ণসংখ্যা ও ভগ্নাংশই মূলদ সংখ্যা।
অমূলদ সংখ্যা (Irrational Number): যে সকল সংখ্যাকে আকারে প্রকাশ করা যায় না, যেখানে p ও q পূর্ণসংখ্যা এবং q ≠ 0, সে সকল সংখ্যাকে অমূলদ সংখ্যা বলে। পূর্ণবর্গ নয় এরূপ যে কোনো স্বাভাবিক সংখ্যার বর্গমূল কিংবা তার ভগ্নাংশ একটি অমূলদ সংখ্যা। যেমন: √2 = 1.414213…., কোনো অমূলদ সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত হিসেবে প্রকাশ করা যায় না।
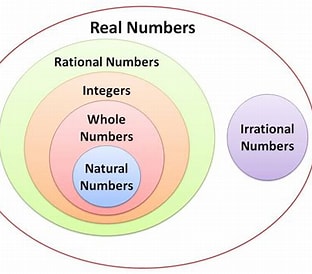
বাস্তব সংখ্যার শ্রেণিবিন্যাস
বাস্তব সংখ্যা (Real Number): সকল মূলদ ও অমূলদ সংখ্যাকে বাস্তব সংখ্যা বলা হয়।
ধনাত্নক সংখ্যা ( Positive Number ) : শূন্য থেকে বড় সকল বাস্তব সংখ্যাকে ধনাত্নক সংখ্যা বলা হয়।
ঋণাত্নক সংখ্যা ( Negative Number ) : শূন্য থেকে ছোট সকল বাস্তব সংখ্যাকে ঋণাত্নক সংখ্যা বলা হয়।
অঋণাত্নক সংখ্যা (Non- Negative Number) : শূন্যসহ সকল ধনাত্নক সংখ্যাকে অঋণাত্নক সংখ্যা বলা হয়।
নিচের চিত্রে বাস্তব সংখ্যার শ্রেণিবিন্যাস দেখানো হল:
বিভিন্ন প্রতিযোগিতামূলক পরীক্ষার প্রশ্ন ও সমাধান
বিভিন্ন প্রতিযোগিতামূলক পরীক্ষার প্রশ্নোত্তর
বিষয়: গাণিতিক যুক্তি
অধ্যায়: বাস্তব সংখ্যা mcq প্রশ্ন উত্তর অনুশীলন
মোট প্রশ্ন: (৩৮)
১. ১ থেকে ১০ পর্যন্ত সংখ্যার মধ্যে মৌলিক সংখ্যা কয়টি ? [ মৎস্য অধিদপ্তরের সাঁটমুদ্রাক্ষরিক কাম-কম্পিউটার অপারেটর : ২১ ]
·
৪
·
৩
·
৬
·
৫
ব্যাখ্যা: ১ থেকে ১০ পর্যন্ত মেীলিক সংখ্যা আছে মোট ৪ টি। যথা: ২,৩,৫ এবং ৭ ।
২. ১ হতে ৩০ পর্যন্ত কয়টি মৌলিক সংখ্যা আছে ? [ তথ্য মন্ত্রণালয়ের অধীন বিটিভি-এর সহকারী প্রকৌশলী (সিভিল) - ১৭ ]
·
৮টি
·
৯টি
·
১০টি
·
১১টি
ব্যাখ্যা: ১ থেকে ৩০ পর্যন্ত মেীলিক সংখ্যা আছে মোট ১০ টি। যথা: ২,৩,৫,৭,১১,১৩,১৭,১৯,২৩ ও ২৯ ।
৩. ৪৩ থেকে ৬০ পর্যন্ত মৌলিক সংখ্যা কয়টি ? [ উত্তরা ব্যাংকের সহকারী অফিসার ( ক্যাশ) : ২০০৮ ]
·
৫
·
৩
·
৭
·
৪
ব্যাখ্যা: ৪৩ থেকে ৬০ পর্যন্ত মেীলিক সংখ্যা আছে মোট ৪ টি। যথা: ৪৩,৪৭,৫৩,৫৯ ।
৪. ৩০ থেকে ৮০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যার ব্যবধান কত ? [ সাধারণ বীমা কর্পোরেশনের জুনিয়র অফিসার : ১৬ ]
·
৩৫
·
৪২
·
৪৮
·
৫৫
ব্যাখ্যা: ৩০ থেকে ৮০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যা = ৭৯ ও ৩১ । পার্থক্য = ৭৯-৩১ = ৪৮ ।
৫. ১০ থেকে ৬০ পর্যন্ত যে মৌলিক সংখ্যাগুলোর একক স্থানীয় অঙ্ক ৯ , তাদের সমষ্টি কত ? [ ২৯ তম বিসিএস ]
·
১৪৬
·
৯৩
·
১০৫
·
১০৭
ব্যাখ্যা: এখানে একক স্থানীয় অঙ্ক ৯ অর্থ শেষের অঙ্কটি ৯ হতে হবে। ১০ থেকে ৬০ পর্যন্ত এরকম সংখ্যা আছে মোট ৫টি।যেমন: ১৯,২৯,৩৯,৪৯ এবং ৫৯ কিন্তু এদের মধ্যে ৩৯ ও ৪৯ মৌলিক নয়।তাই মৌলিক সংখ্যা তিনটি ১৯,২৯ এবং ৫৯ এর যোগফল হবে = ১৯+২৯+৫৯ = ১০৭ ।
৬. নিচের কোনটি মৌলিক সংখ্যা নয় ? [ মাদকদ্রব্য নিয়ন্ত্রণ অধিদপ্তরের ওয়েরলেস অপারেটর : ২১ ]
·
২৬৩
·
২৩৩
·
২৫৩
·
২৪১
ব্যাখ্যা: প্রদত্ত সংখ্যাগুলোর মধ্যে ২৫৩ কে ভাঙ্গলে ১১×২৩ = ২৫৩ হয় । কিন্তু অন্য সংখ্যাগুলোকে ভাঙ্গানো যায় না।। তাই ২৫৩ সংখ্যাটি মৌলিক সংখ্যা নয়।
৭. ২৫ থেকে ৫৫ এর মধ্যে মৌলিক সংখ্যা কয়টি ? [ সহকারী উপজেলা /থানা শিক্ষা অফিসার : ১৬ ]
·
৭টি
·
৬টি
·
৪টি
·
৫টি
ব্যাখ্যা: ২৫ থেকে ৫৫ এর মধ্যে মৌলিক সংখ্যা আছে = ৭টি।যথা: ২৯,৩১,৩৭,৪১,৪৩,৪৭,৫৩ ।
৮. নিচের কোনটি মৌলিক সংখ্যা ? [ ১৩ তম বেসরকারি প্রভাষক নিবন্ধন পরীক্ষা : ১৬ ]
·
৯১
·
৮৭
·
৬৩
·
৫৯
ব্যাখ্যা: যে সংখ্যাকে ১ ও সেই সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না, তাকে মৌলিক সংখ্যা বলে। এখানে ৫৯ মৌলিক সংখ্যা ।
৯. নিচের কোন সংখ্যাটি মৌলিক ? [ উপ-সহকারী প্রকৌশলী (সিভিল) : ১৫ ]
·
৪৯
·
৫১
·
৫৩
·
৫৫
ব্যাখ্যা: যে সংখ্যাকে ১ ও সেই সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না, তাকে মৌলিক সংখ্যা বলে। এখানে ৫৩ মৌলিক সংখ্যা ।
১০. ৬০ থেকে ৮০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যার অন্তর কত ? [ ৭ম বেসরকারি প্রভাষক নিবন্ধন পরীক্ষা : ১১ ]
·
৮
·
১২
·
১৮
·
১৪
ব্যাখ্যা: ৬০ ও ৮০ এর মধ্যে সর্বনিম্ন ও সর্বোচ্চ মৌলিক সংখ্যা হচ্ছে যথাক্রমে ৬১ ও ৭৯। সুতরাং এ দুটি সংখ্যার অন্তর হবে (৭৯ - ৬১) = ১৮।
১১. ৩০ থেকে ৯০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যার অন্তর কত ? [ বহিরাগমন ও পার্সপোর্ট অধিদপ্তরের সহকারী পরিচালক : ১১ ]
·
৪৬
·
৪৮
·
৫২
·
৫৮
ব্যাখ্যা: ৩০ থেকে ৯০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যা হচ্ছে ৮৯ ও ৩১। এদের অন্তর = ৮৯– ৩১ = ৫৮।
১২. ৩০ থেকে ৮০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যার ব্যবধান কত ? [ সাধারণ বীমা কর্পোরেশনের জুনিয়র অফিসার : ১৬ ]
·
৩৫
·
৪২
·
৪৮
·
৫৫
ব্যাখ্যা: ৩০ থেকে ৮০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যা = ৭৯ ও ৩১ । পার্থক্য = ৭৯-৩১ = ৪৮ ।
১৩. নিচের কোনটি মৌলিক সংখ্যা ? [ সাধারণ বীমা কর্পোরেশনের জুনিয়র অফিসার : ১৬ ]
·
৭২
·
৮৭
·
৬৩
·
কোনটিই নয়
ব্যাখ্যা: যে সংখ্যাকে ১ ও ঐ সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না, তাকে মৌলিক সংখ্যা বলে। এখানে কোনটিই মৌলিক সংখ্যা নয়।
১৪. নিচের কোন সংখ্যাটি মৌলিক ? [ ১০ তম বিসিএস ]
·
৯১
·
১৪৩
·
৪৭
·
৮৭
ব্যাখ্যা: যে সংখ্যাকে ১ ও ঐ সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না, তাকে মৌলিক সংখ্যা বলে। এখানে ৪৭ মৌলিক সংখ্যা ।
১৫. নিচের কোনটি মৌলিক সংখ্যা ? [ সমাজসেবা অধিদপ্তরের সহকারী শিক্ষক : ১৭ ]
·
৯
·
৮
·
৪
·
২
ব্যাখ্যা: যে সংখ্যাকে ১ ও ঐ সংখ্যা ছাড়া অন্য কোনো সংখ্যা দ্বারা ভাগ করা যায় না, তাকে মৌলিক সংখ্যা বলে। এখানে ২ মৌলিক সংখ্যা ।
১৬. ৩০ থেকে ৪০ এর মধ্যবর্তী বৃহত্তম ও ক্ষুদ্রতম মৌলিক সংখ্যার ব্যবধান কত ? [ পল্লী উন্নয়ন ও সমবায় বিভাগের একটি বাড়ি একটি খামার প্রকল্পের উপজেলা সমন্বয়কারী : ১৭ ]
·
৫
·
৬
·
৯
·
৭
ব্যাখ্যা: ৩০ থেকে ৪০ এর মধ্যে বৃহত্তম মৌলিক সংখ্যা ৩৭
৩০ থেকে ৪০ এর মধ্যে ক্ষুদ্রতম মৌলিক সংখ্যা ৩১
ব্যবধান = ৩৭ - ৩১ = ৬
১৭. জোড় মৌলিক সংখ্যা কয়টি ? [ মৎস্য অধিদপ্তর কর্মচারী নিয়োগ। অফিস সহায়ক : ২১ ]
·
১টি
·
২টি
·
৩টি
·
কোনটিই নয়
ব্যাখ্যা: মৌলিক সংখ্যা সবগুলোই বিজোড় শুধু ২ একটি জোড় সংখ্যা।
১৮. ২ এবং ৩২ এর মধ্যে মৌলিক সংখ্যা কয়টি ? [ সরকারি মাধ্যমিক বিদ্যালয় সহকারী শিক্ষক : ১১ ]
·
৮টি
·
৯টি
·
১০টি
·
১১টি
ব্যাখ্যা: ২ এবং ৩২ এর মধ্যে মৌলিক সংখ্যাগুলো হলো = ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১ = ১০ টি। তবে ২ থেকে ৩২ এর মধ্যে মৌলিক সংখ্যাগুলো হলো = ২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১ = ১১ টি।
১৯. ৯০ থেকে ১০০ এর মধ্যে কয়টি মৌলিক সংখ্যা আছে ? [ প্রতিরক্ষা মন্ত্রণালয়ের সিভিলিয়ান স্টাফ অফিসার এবং সহকারী পরিচালক : ২০১৬ ]
·
৩টি
·
২টি
·
১টি
·
একটিও নেই
ব্যাখ্যা: ৯০ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যা হলো - ১ টি যথা ৯৭।
২০. ৫০ এর চেয়ে ছোট কয়টি মৌলিক সংখ্যা আছে ? [ জেলা প্রাথমিক শিক্ষা অফিসার, পিটিআই এর সুপারিনটেনডেন্ট, পিটিআই এর সহকারী সুপারিনটেনডেন্ট : ২০০৫ ]
·
১৪টি
·
১৫টি
·
১৬টি
·
১৭টি
ব্যাখ্যা: ৫০ এর চেয়ে ছোট মৌলিক সংখ্যা মোট ১৫ টি। সেগুলো হলোঃ ২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১, ৩৭, ৪১, ৪৩ ও ৪৭।
২১. কোন ধরনের সংখ্যা ? [ নবম-দশম শ্রেণি (মাধ্যমিক গণিত) ]
·
স্বাভাবিক
·
মূলদ
·
অমূলদ
·
মৌলিক
ব্যাখ্যা: সব ধরনের সাধারণ ভগ্নাংশ মুলদ সংখ্যা হয় । তবে পৌনঃপুনিক থেকে আসা সাধারণ ভগ্নাংশসমূহ মূলদ সংখ্যা নয় ।
২২. নিচের কোন দুটি সহ মৌলিক সংখ্যা ? [ ১১ তম বেসরকারি প্রভাষক নিবন্ধন পরীক্ষা ]
·
২৭,৫৪
·
৬৩,৯১
·
১৮৯,২১০
·
৫২,৯৭
ব্যাখ্যা: প্রদত্ত অপশনে (ঘ) ৫২,৯৭ ক্রমজোড়টি সহমৌলিক। কারণ, ৫২ = ১×২×২×১৩ এবং ৯৭ = ১×৯৭ দেখা যাচ্ছে ৫২ ও ৯৭ এর ১ ভিন্ন অন্য কোনো সাধারণ উৎপাদক নেই। সুতরাং এরা পরস্পর সহমৌলিক।
২৩. m ও n বিজোড় সংখ্যা হলে নিচের কোনটি জোড় ? [ বাংলাদেশ ট্যারিফ কমিশনের গবেষণা কর্মকর্তা : ২০১৮ ]
·
mn
·
mn+1
·
mn+2
·
mn+4
ব্যাখ্যা: ধরি, m = 1, n = 3
∴ (ক) 1x3 = 3, যা বিজোড় সংখ্যা
(খ) 1 × 3 + 1 = 4, যা জোড় সংখ্যা
(গ) 1 × 3 + 2 = 5, যা বিজোড় সংখ্যা
(ঘ) 1 × 3 + 4 = 7, যা বিজোড় সংখ্যা ।
সুতরাং, mn + 1 অবশ্যই জোড় সংখ্যা হবে।
২৪. যদি n একটি জোড় সংখ্যা হয় তবে নিচের কোনটি জোড় সংখ্যা হতে পারবে না ? [ দুর্নীতি দমন কমিশনে উপসহকারী পরিচালক : ২০১০ ]
·
·
3(n+1)+3
·
2n+2
·
2n+3
ব্যাখ্যা: 3 একটি বিজোড় সংখ্যা হওয়ায়,একই সাথে 2 জোড় সংখ্যা হওয়ায় দুটি সংখ্যার যোগফল সবসময়ই বিজোড় হবে।
২৫. নিচের কোনটি অবশ্যই জোড় সংখ্যা ? [ আইন, বিচার ও সংসদ বিষয়ক মন্ত্রণালয়ের সাব-রেজিস্ট্রার : ২০১২ ]
·
x+y
·
x+y+1
·
xy+2
·
2x
ব্যাখ্যা: 2 × বিজোড় = জোড় সংখ্যা হয়। যেমন, ২ × ৩ = ৬
২৬. যদি n একটি জোড় সংখ্যা হয় তবে নিচের কোনটি জোড় সংখ্যা হতে পারবে না ? [ পরিসংখ্যান ব্যুরোর জুনিয়র পরিসংখ্যান সহকারী : ২০১৬ ]
·
·
5(n+2)
·
2n+2
·
7n+3
ব্যাখ্যা: ধরি n = 2 । তাহলে (7×2)+3 = 14 + 3 = 17 যা একটি বিজোড় সংখ্যা ।
২৭. ০,১,২,৩ দ্বারা গঠিত বৃহত্তম ও ক্ষুদ্রতম সংখ্যার মধ্যে পার্থক্য কত হবে ? [ খনিজ সম্পদ মন্ত্রণালয় সহকারী সচিব/সহকারী পরিচালক (প্রশাসন) : ২০১৯ ]
·
৩০৮৭
·
২০৮৭
·
৩১৮৭
·
২১৮৭
ব্যাখ্যা: ০ দ্বারা কোন সংখ্যা শুরু হয় না।তাই ক্ষুদ্রতম সংখ্যা তৈরির ক্ষেত্রে প্রথমে ১ বসিয়ে তারপর ০ বসাতে হবে; তাই ক্ষুদ্রতম সংখ্যাটি হবে ১০২৩ এবং বৃহত্তম সংখ্যাটি হবে ৩২১০ । সুতরাং পার্থক্য ৩২১০-১০২৩ = ২১৮৭ ।
২৮. ০,১,২,৩ ও ৪ দ্বারা গঠিত পাঁচ অঙ্কের বৃহত্তম ও ক্ষুদ্রতম সংখ্যার যোগফল কোনটি ? [ ডাক ও টেলিযোগাযোগ বিভাগের অধীন ডাক অধিদপ্তরের এস্টিমেটর : ২০১৮ ]
·
৪৪৪৪৪
·
৫৩৪৪২
·
৫৩৪৪৪
·
৫৩৪৪৮
ব্যাখ্যা: ০,১,২,৩ ও ৪ দ্বারা গঠিত পাঁচ অঙ্কের বৃহত্তম সংখ্যা ৪৩২১০ । ০,১,২,৩ ও ৪ দ্বারা গঠিত পাঁচ অঙ্কের ক্ষুদ্রতম সংখ্যা ১০২৩৪ সুতরাং যোগফল = ( ৪৩২১০+১০২৩৪ ) = ৫৩৪৪৪ ।
২৯. তিন অংকের বৃহত্তম সংখ্যা ও ক্ষুদ্রতম সংখ্যার পার্থক্য কত ? [ বাংলাদেশ রেলওয়ের উপসহকারী প্রকৌশলী (সিভিল) : ১৬ ]
·
৯৯৮
·
৯৮৮
·
৮৯৯
·
৮৮৮
ব্যাখ্যা: তিন অঙ্কের বৃহত্তম সংখ্যা - তিন অঙ্কের ক্ষুদ্রতম সংখ্যা = ৯৯৯ - ১০০ = ৮৯৯
৩০. পাঁচ অঙ্কের ক্ষুদ্রতম সংখ্যা ও চার অঙ্কের বৃহত্তম সংখ্যার অন্তর কত ? [ প্রতিরক্ষা মন্ত্রণালয়ের সিভিলিয়ান স্টাফ অফিসার এবং সহকারী পরিচালক : ২০১৬ ]
·
৯৮৯৯৯
·
১০
·
১
·
১০০
ব্যাখ্যা: পাঁচ অংকের ক্ষুদ্রতম সংখ্যা = ১০০০০ , চার অঙ্কের বৃহত্তম সংখ্যা = ৯৯৯৯ , তাহলে, ১০০০০ - ৯৯৯৯ = ১
৩১. ১-১০০ পর্যন্ত মৌলিক সংখ্যা কয়টি ? [ বিভিন্ন মন্ত্রণালয়ের সহকারী প্রোগ্রামার : ১৭ ]
·
২৩টি
·
২৫টি
·
২৭টি
·
২৯টি
ব্যাখ্যা: ১ থেকে ১০০ পর্যন্ত মৌলিক সংখ্যাগুলো হলো: ২, ৩, ৫, ৭, ১১, ১৩, ১৭, ১৯, ২৩, ২৯, ৩১, ৩৭, ৪১, ৪৩, ৪৭, ৫৩, ৫৯, ৬১, ৬৭, ৭১, ৭৩, ৭৯, ৮৩, ৮৯ ও ৯৭। মোট ২৫ টি।
৩২. ১ থেকে ১০ পর্যন্ত জোড় মৌলিক সংখ্যা কয়টি ? [ মৎস্য অধিদপ্তর কর্মচারী নিয়োগ। অফিস সহায়ক : ২১]
·
২
·
১
·
৩
·
৪
ব্যাখ্যা: ১ থেকে ১০ পর্যন্ত মৌলিক সংখ্যা চারটি। ২, ৩, ৫, এবং ৭। শুধু ২ একটি জোড় সংখ্যা।
৩৩. নিচের কোন ক্রমজোড়টি সহমৌলিক ? [ ১১ তম বেসরকারি প্রভাষক নিবন্ধন পরীক্ষা : ২০১৪ ]
·
(৪, ৬)
·
(৬, ৯)
·
(৯, ১২)
·
(১২, ১৭)
ব্যাখ্যা: প্রদত্ত অপশনে (ঘ) ১২,১৭ ক্রমজোড়টি সহমৌলিক। কারণ, ১২ = ১×৩×২×২ এবং ১৭ = ১×১৭ দেখা যাচ্ছে ১২ ও ১৭ এর ১ ভিন্ন অন্য কোনো সাধারণ উৎপাদক নেই। সুতরাং এরা পরস্পর সহমৌলিক।
৩৪. কোনটি স্বাভাবিক সংখ্যা ? [ নবম-দশম শ্রেণি (মাধ্যমিক গণিত) ]
·
-1
·
·
·
3
ব্যাখ্যা: ১ , ২ , ৩ ..... এগুলো স্বাভাবিক সংখ্যা
৩৫. ক্ষুদ্রতম মৌলিক সংখ্যা নিচের কোনটি ? [ নবম-দশম শ্রেণি (মাধ্যমিক গণিত) ]
·
১
·
২
·
৩
·
৫
ব্যাখ্যা: ২ সবচেয়ে ছোট মৌলিক সংখ্যা
৩৬. সকল মূলদ ও অমূলদ সংখ্যাকে কি বলে ? [ নবম-দশম শ্রেণি (মাধ্যমিক গণিত) ]
·
স্বাভাবিক সংখ্যা
·
মৌলিক সংখ্যা
·
পূর্ণসংখ্যা
·
বাস্তব সংখ্যা
ব্যাখ্যা: সকল মূলদ ও অমূলদ সংখ্যাকে একত্রে বাস্তব সংখ্যা বলে
৩৭. √3 এবং 5 এর মাঝে কয়টি পূর্ণসংখ্যা আছে ? [ নবম-দশম শ্রেণি (মাধ্যমিক গণিত) ]
·
1টি
·
2টি
·
3টি
·
4টি
ব্যাখ্যা: √3 = 1.73205080757 এবং 5 এর মাঝে 2 , 3 , 4 এই তিনটি পূর্ণসংখ্যা আছে ।
৩৮. কোন ধরনের সংখ্যা ? [ নবম-দশম শ্রেণি (মাধ্যমিক গণিত) ]
·
মূলদ
·
অমূলদ
·
স্বাভাবিক
·
অনাবৃত দশমিক
ব্যাখ্যা: সব ধরনের সাধারণ ভগ্নাংশ মুলদ সংখ্যা হয় । তবে পৌনঃপুনিক থেকে আসা সাধারণ ভগ্নাংশসমূহ মূলদ সংখ্যা নয় ।